Camera-Lidar Extrinsic Calibration from Mutual Information: D2D vs I2I (with vectorized implementation)
Python implementation (with vectorization) for MI-based Camera-Lidar extrinsic calibration.
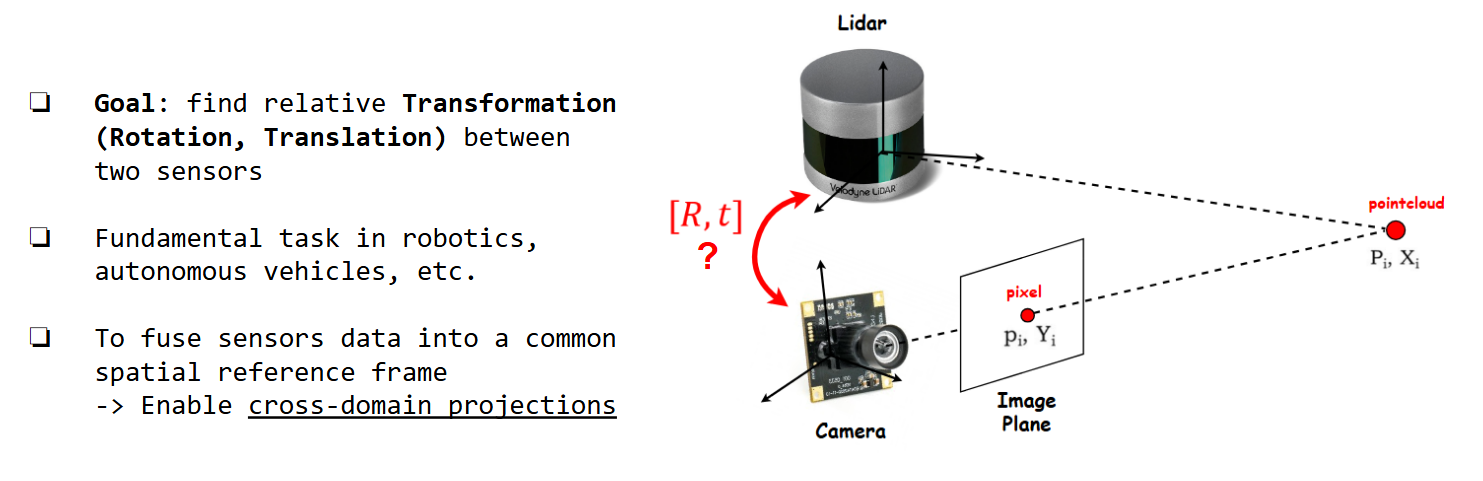
Goals
In this post, we want to obtain the following:
- Basic concept of Extrinsic Calibration
- Feature Extraction -based vs Mutual Information (MI) -based Extrinsic Calibration
- Python implementation of MI-based method (w/ vectorization) -> easier + faster to debug/visualize results
My source code is available here.
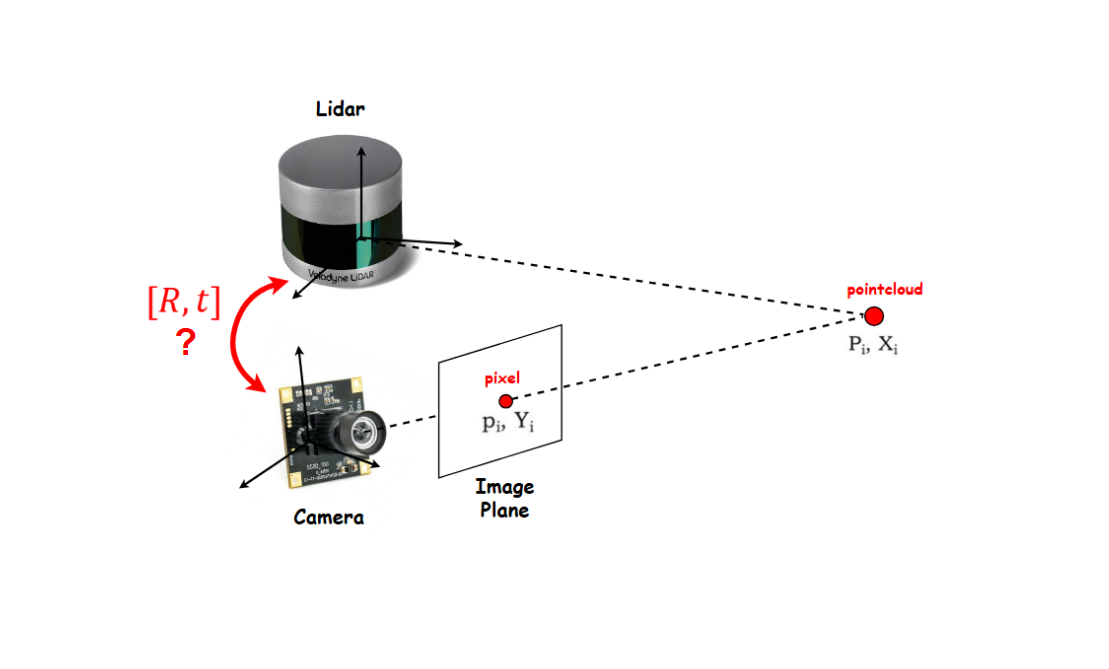
Extrinsic Calibration Concept
Extrinsic Calibration Concept
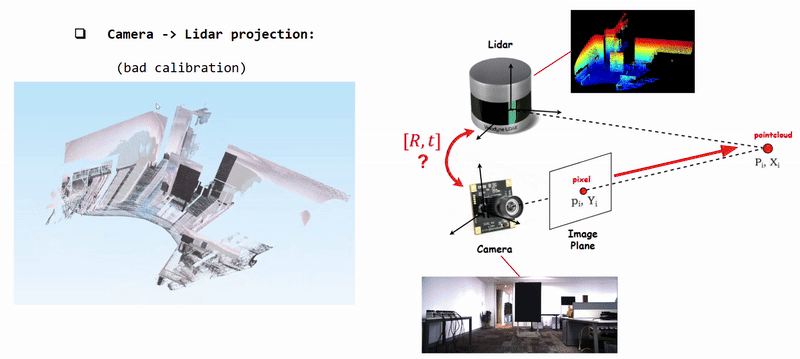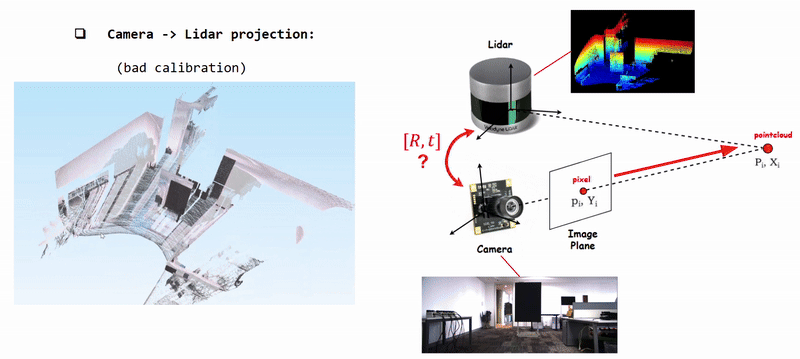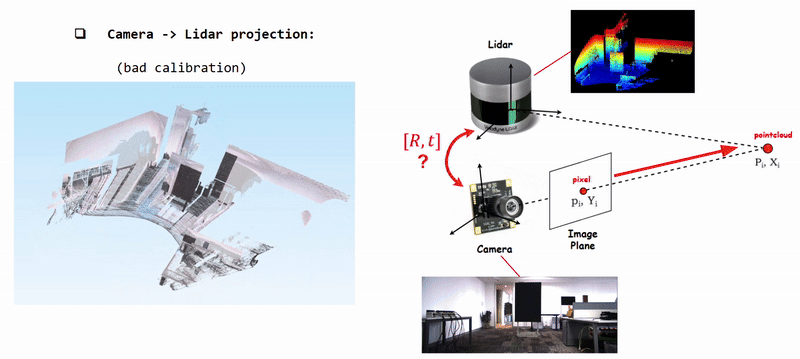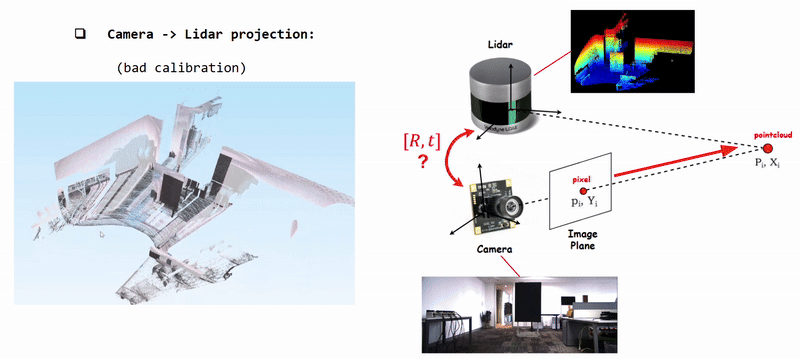Projecting Camera Pixels (Color) onto Lidar Pointcloud using poorly calibrated [R|t]
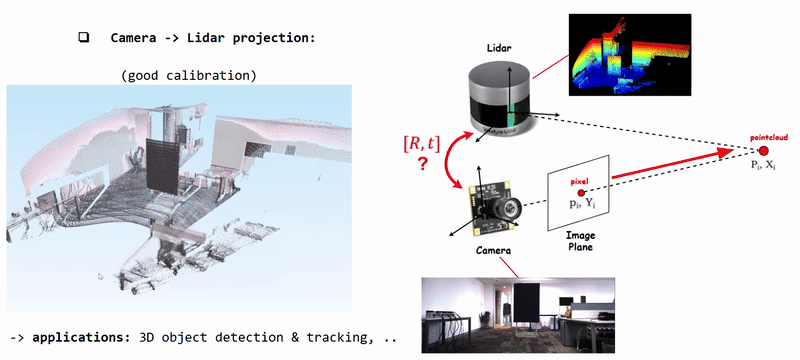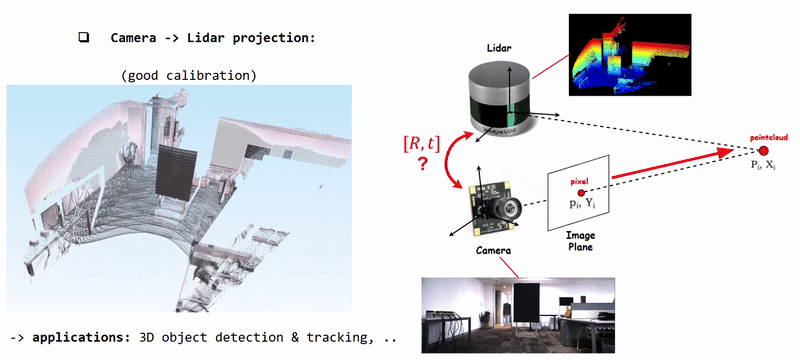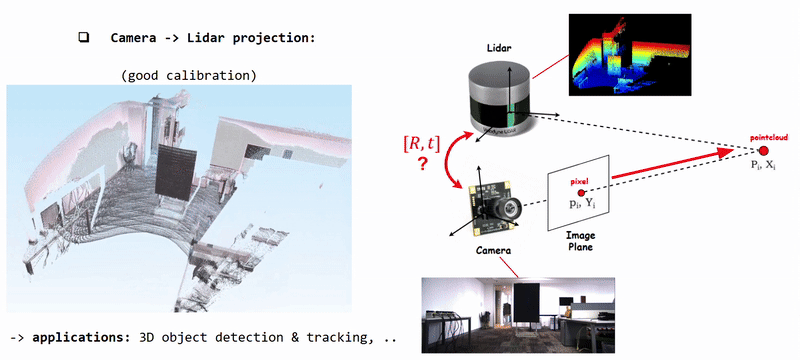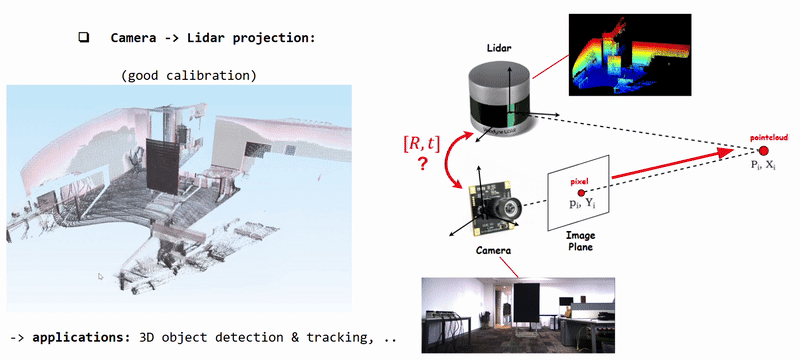Projecting Camera Pixels (color information) onto Lidar Pointcloud using well calibrated [R|t]
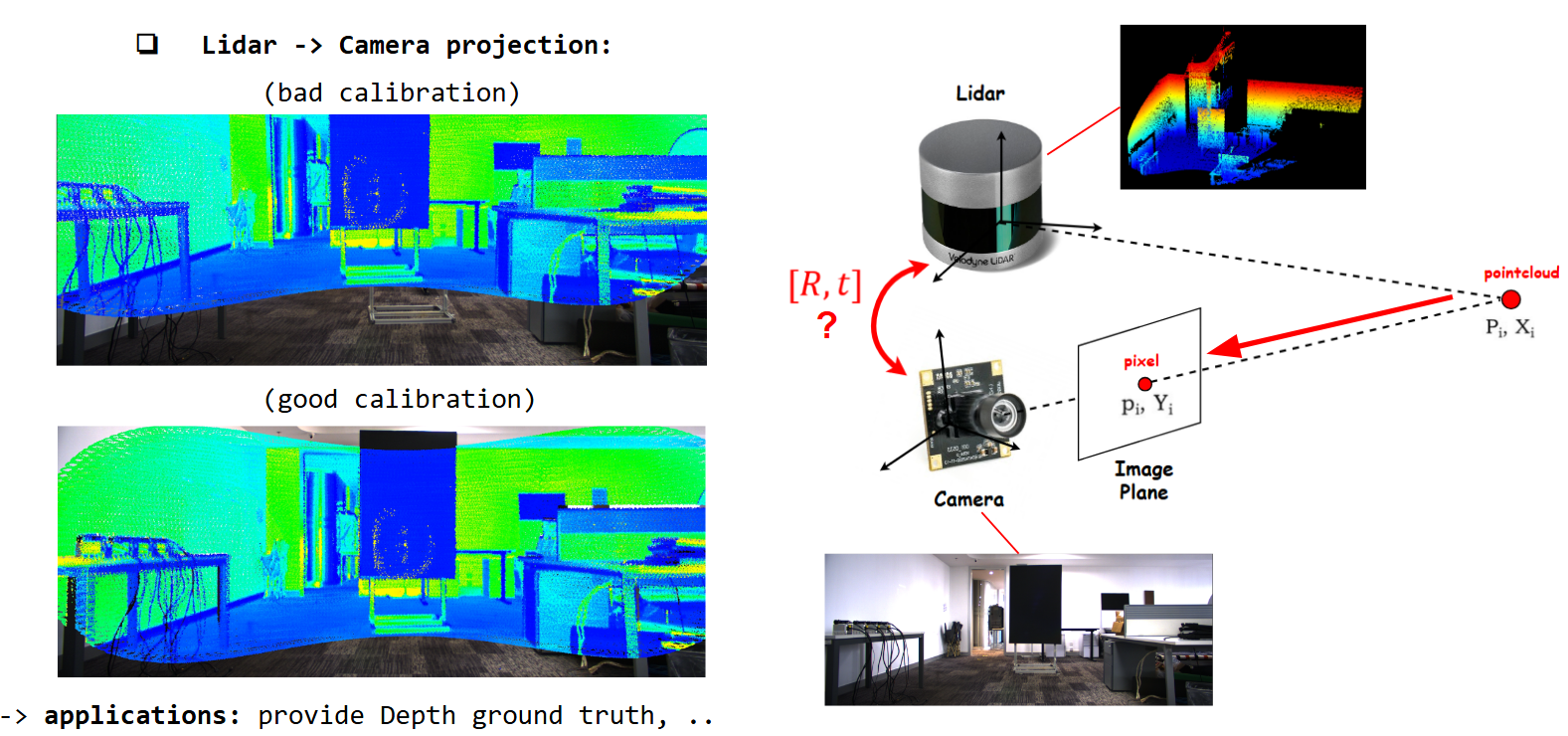Projecting Lidar Pointcloud (intensity + depth information) onto Camera Image using calibrated [R|t]
Therefore, we need accurate extrinsic calibration to obtain effective sensor fusion.
-> How do we calibrate ?
Feature Extraction -based (Target -based)
This approach has three main steps: 1) features extraction, 2) features matching, 3) reprojection error optimization
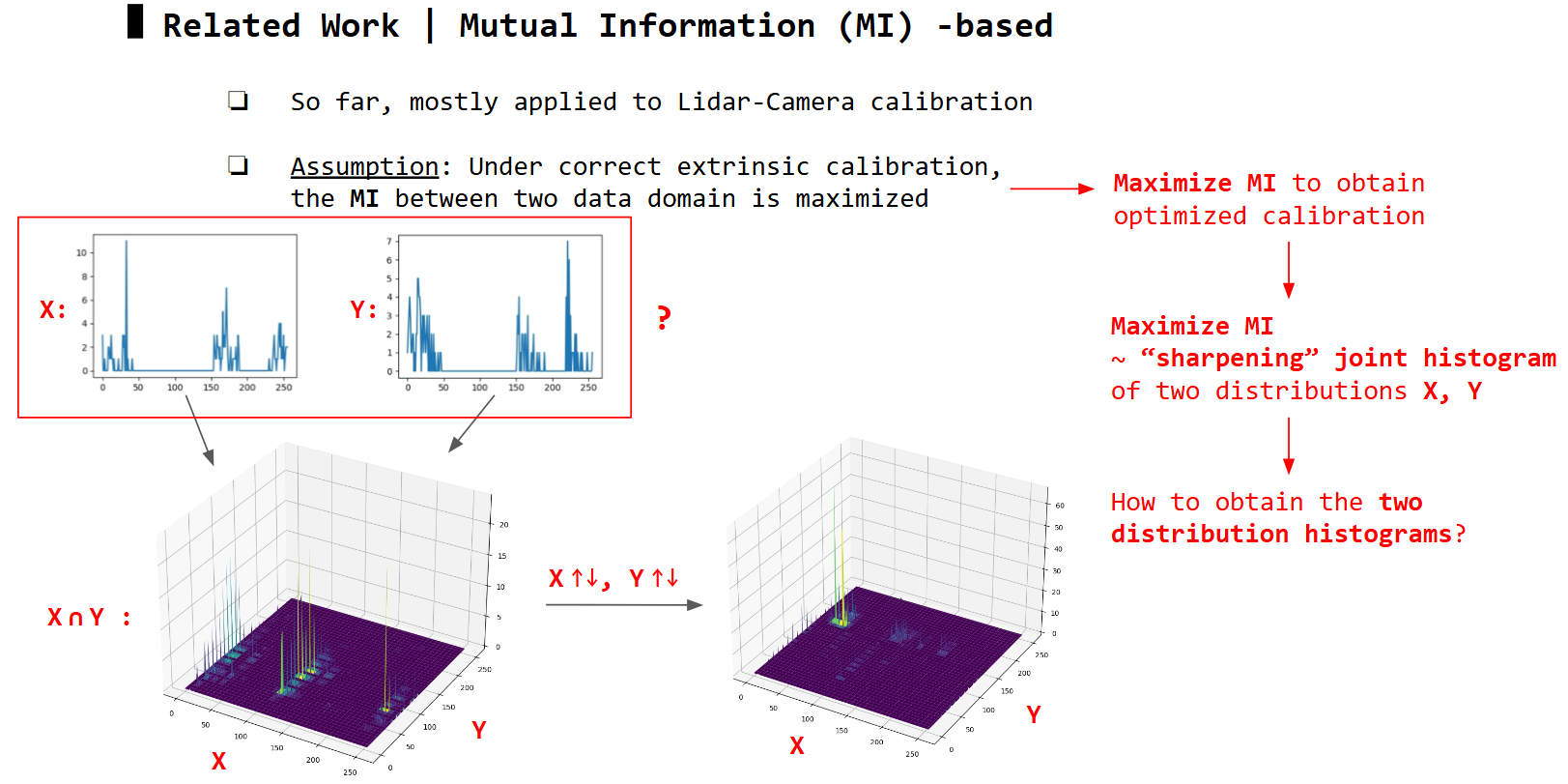
Mutual Information (MI) -based
Unlike target -based methods, target-free methods use only sensor data:
Utilzing mutual information is also one of target-free methods: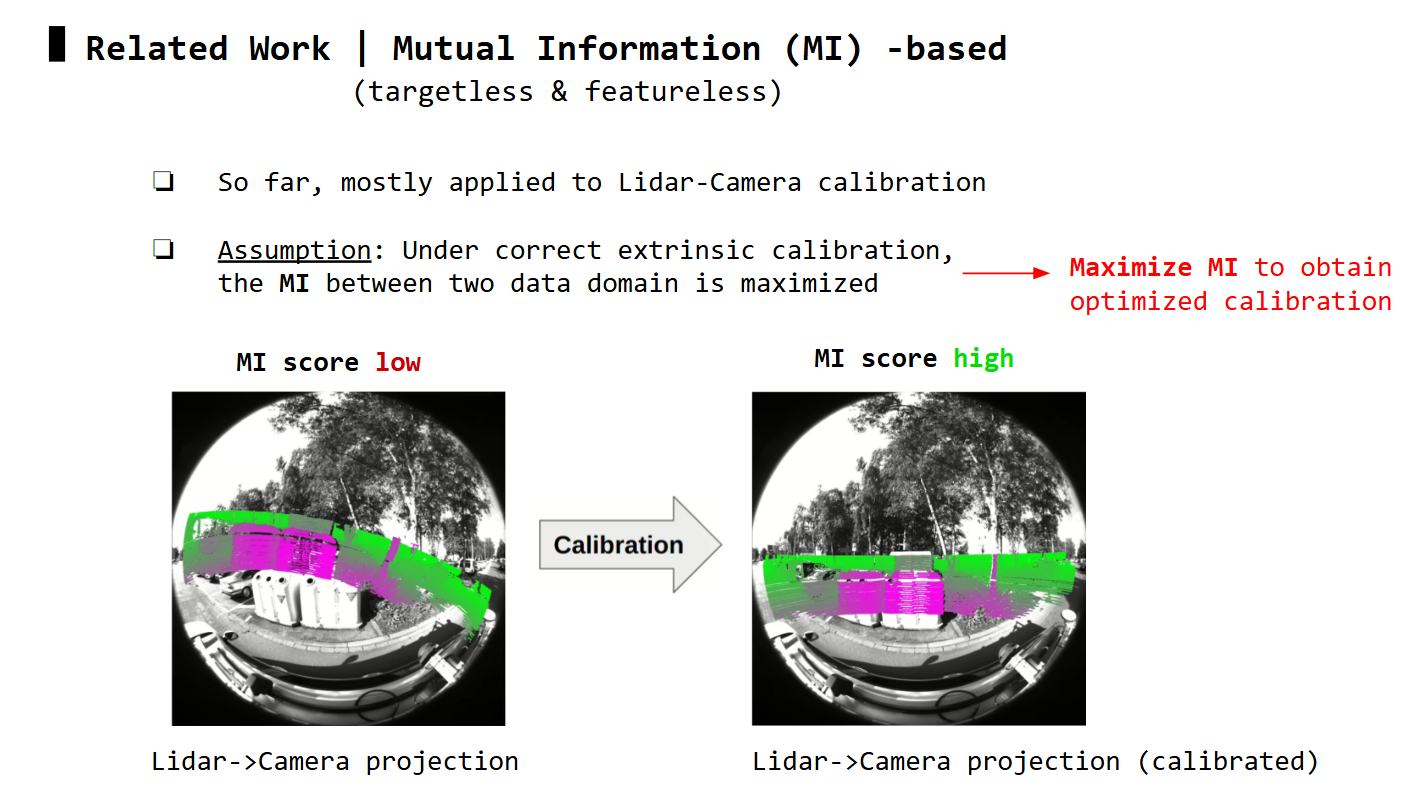 
Based on the underlying formulation of the two distributions X & Y, MI-based methods can be categorized into intensity-to-intensity (I2I) or depth-to-depth (D2D) methods.
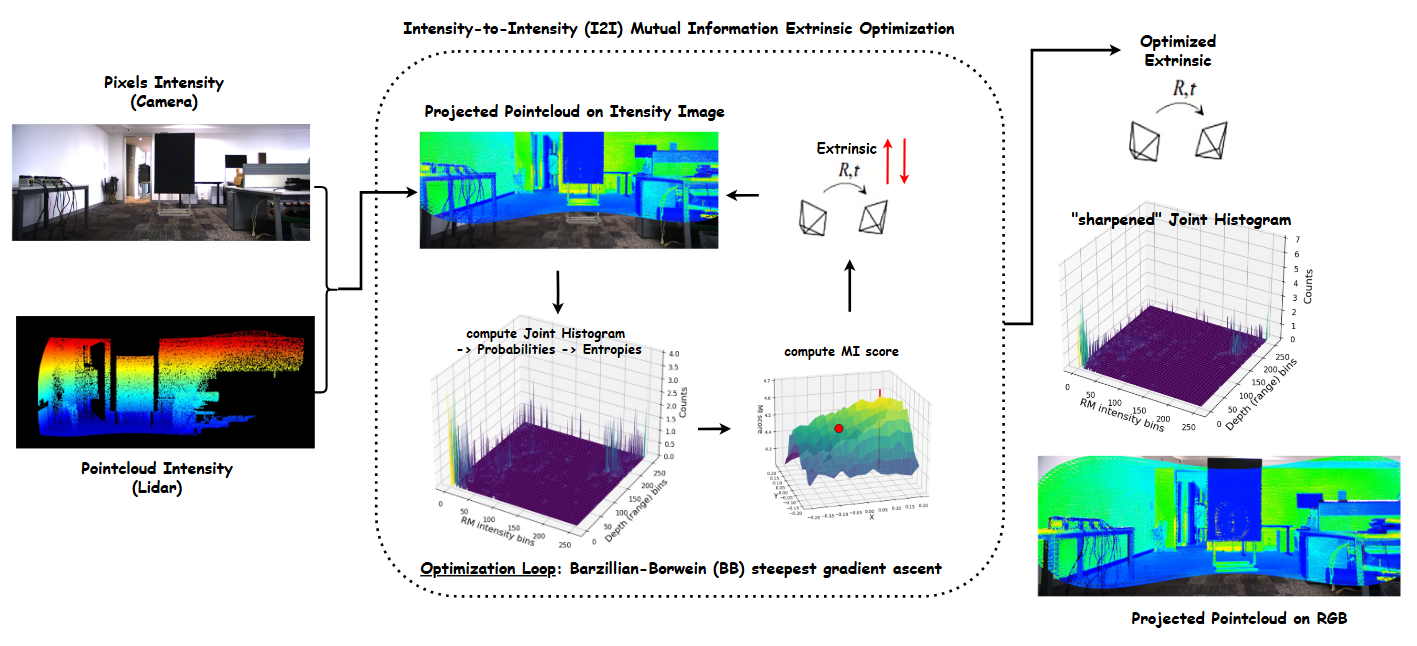
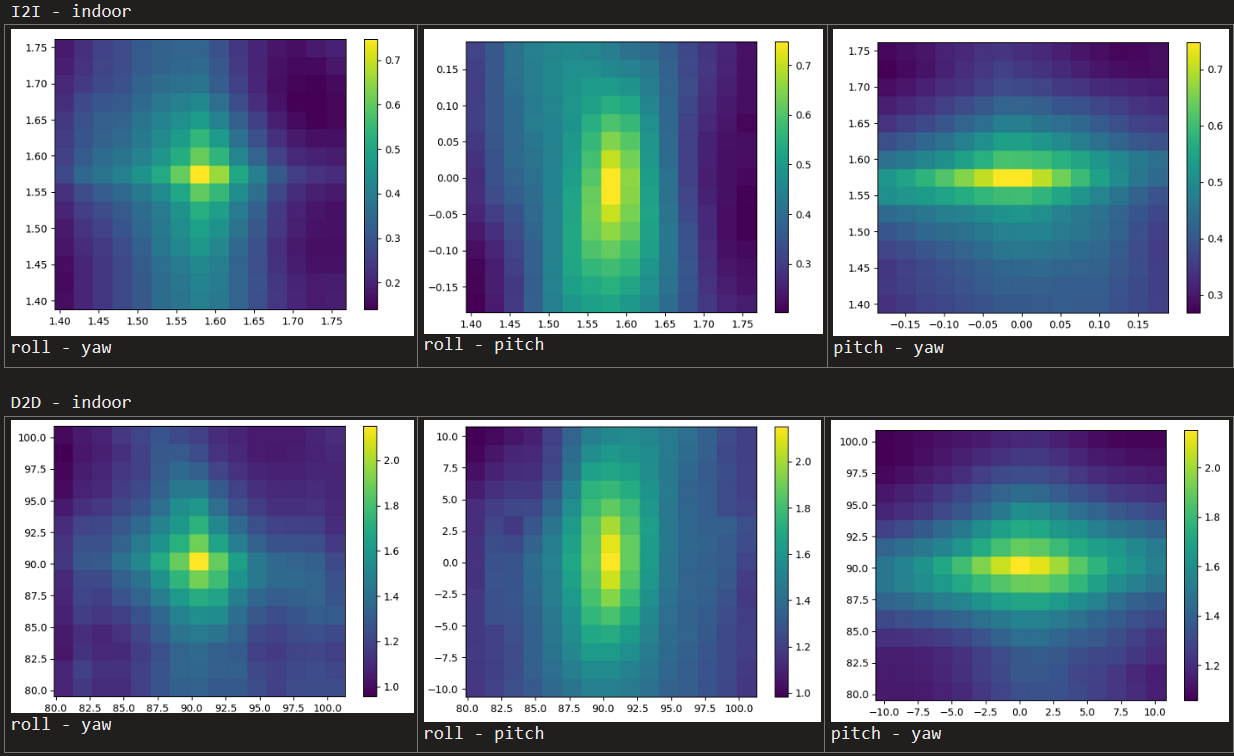
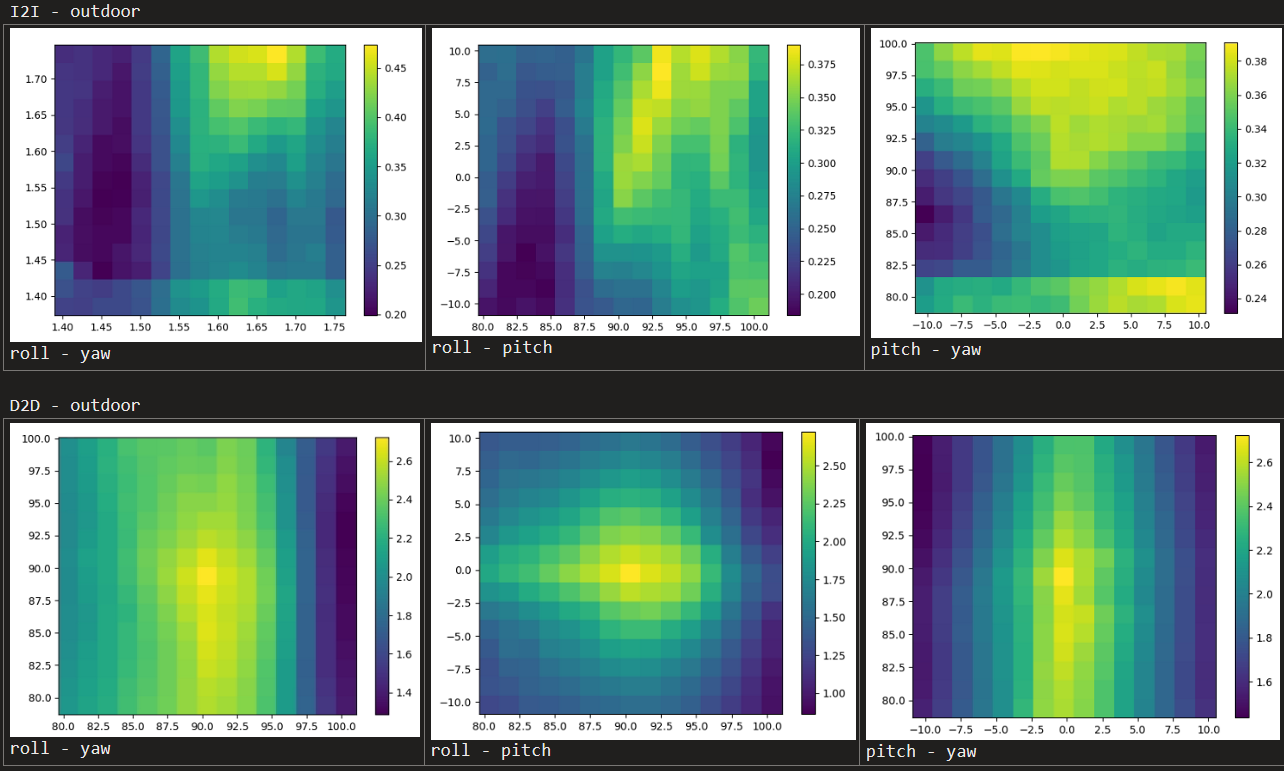
Intensity-to-Intensity (I2I)
Experiments show the I2I calibrated results can converge well and be stable in indoor scenes, but performs poorly outdoor. 
Depth-to-Depth (D2D)
D2D method investigated I2I problem, then proposed to utilize depth information instead. 
D2D shows higher mutual information, and has more defined global optimum (good for convergence) than I2I.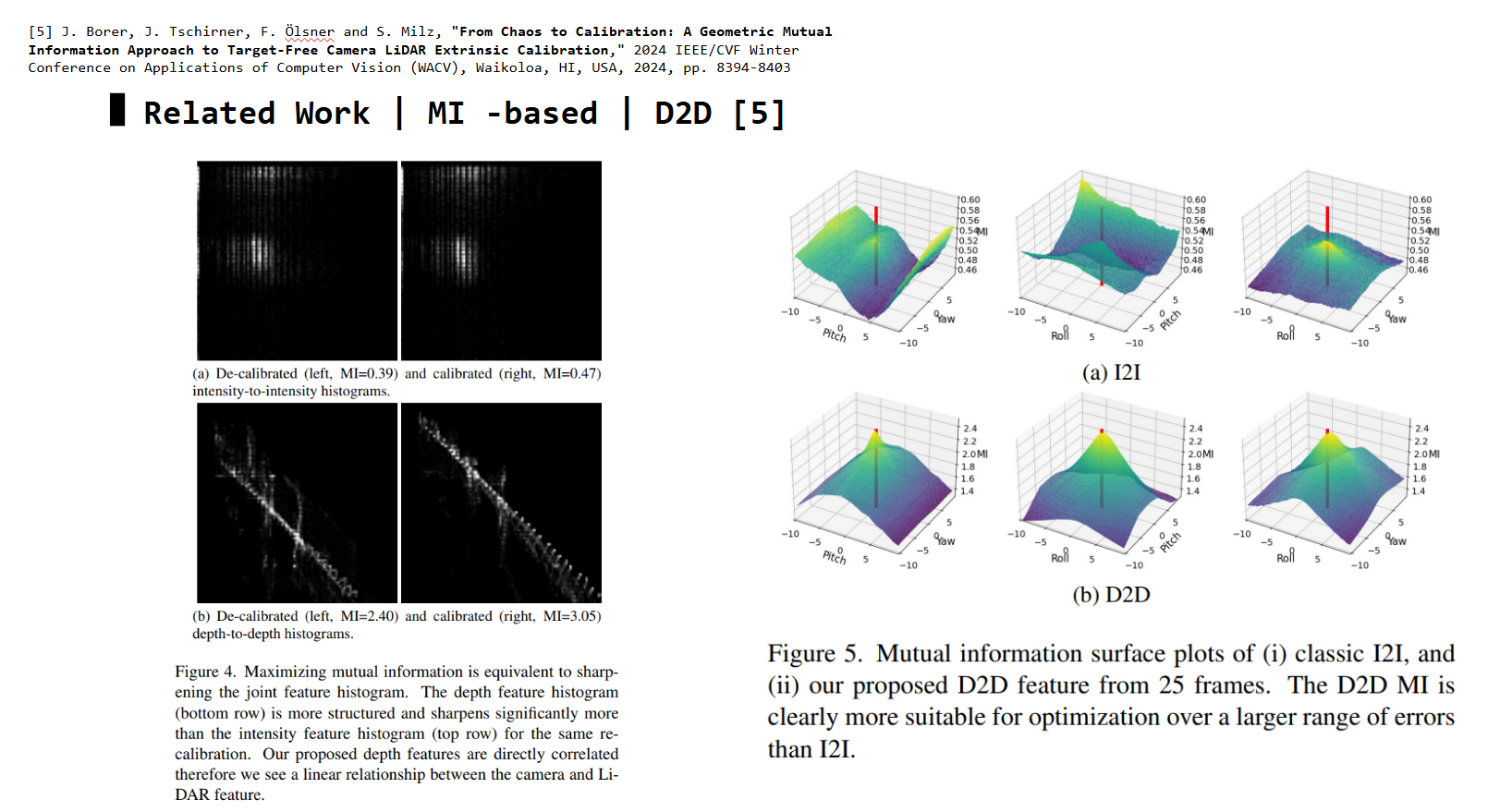 
Optimization Loop: I2I vs D2D
Here is an overview on how the two distribution domains (camera data & lidar data) are used and updated (following the updated extrinsic params) during optimization loop, between I2I and D2D methods:
I2I optimization loop
D2D optimization loop
Now, you have basic understanding of I2I and D2D methods, and their optimization flow, let’s implement them in Python.
Python Implementation of MI -based approach
The most time-consuming steps are “projecting pointcloud onto camera plane” and “computing histograms”, so I will only focus on the code for these parts. You may find the rest of the code in my repo
Non-Vectorized version (for loops)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def compute_hist(self, ext_vec):
###
### ext_vec: x, y, z, roll_rad, pitch_rad, yaw_rad (zyx euler-angle, radian)
###
self.hist_handler.reset()
for i in range(self.N):
for point in self.pointclouds[i]:
px, py, pz, pi = point
point_dist = px**2 + py**2 + pz**2
if (point_dist / DIST_THRES) < 1: # avoid points in inifite
### project point into image
t = ext_vec[:3]
rot = (R.from_rotvec(ext_vec[3] * np.array([1,0,0])) * R.from_rotvec(ext_vec[4] * np.array([0,1,0])) * R.from_rotvec(ext_vec[5] * np.array([0,0,1])) )
T = np.eye(4); T[:3, :3] = rot.as_matrix(); T[:3,3] = t
P_L = [px, py, pz]
p_C = self.utils.project_point_to_image(P_L, T, self.cam_K)
### validate point
if not self.utils.validate_image_point(p_C, self.images[i]):
continue
intensity_bin = int(pi / self.bin_fraction)
gray_bin = int(self.images[i][p_C[1], p_C[0]] / self.bin_fraction)
### update hist
self.hist_handler.intensity_hist[intensity_bin] += 1
self.hist_handler.gray_hist[gray_bin] += 1
self.hist_handler.joint_hist[gray_bin, intensity_bin] += 1
self.hist_handler.intensity_sum += intensity_bin
self.hist_handler.gray_sum += gray_bin
self.hist_handler.total_points += 1
To run this version, enter the following commands:
1
2
cd src/
python script_I2I.py
The complexity of this code is O(N*M), where N is the number of images (usually small, < 100), and M is the number of points in the 3D Lidar pointcloud (significantly large, M » N)
The compute_hist function iterates these three main steps for each point in 3D pointcloud per image: 1) project the point onto image, 2) validate the projected point, 3) updating histograms.
-> We have to vectorize all three steps to eliminate M from computation complexity, meaning to process all points simultaneuously.
Vectorized version
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
def compute_hist(self, ext_vec):
###
### ext_vec: x, y, z, roll_rad, pitch_rad, yaw_rad (zyx euler-angle, radian)
###
self.hist_handler.reset()
for i in range(self.N):
### project P_L to P_C
t = np.array([ext_vec[:3]]).T
rot_mat = (R.from_rotvec(ext_vec[3] * np.array([1,0,0])) * R.from_rotvec(ext_vec[4] * np.array([0,1,0])) * R.from_rotvec(ext_vec[5] * np.array([0,0,1])) ).as_matrix()
pointcloud_C = rot_mat @ self.pointclouds[i].T[:3,:] + t
### project P_C to p_C
p_C = self.cam_K @ pointcloud_C
p_C_ = p_C / p_C[2, :] # normalize with z
p_C_ = p_C_[:2,:]
p_C_[np.isnan(p_C_)] = 999999 # divided by 0 -> outliers
p_C_ = p_C_.astype(int)
delta_C = p_C_ - np.array([[self.image_W, self.image_H]]).T # check if pixel within image
### check: 1) wihin image, 2) non-negative pixel coord, 3) in front of camera
mask_C = (delta_C < 0) & (p_C_ >= 0) & (p_C[2, :] > 0)
mask_C = mask_C[0,:] & mask_C[1,:]
p_C_intensity = np.append(p_C_, np.array([self.pointclouds[i].T[3,:]]), axis=0)
p_C_intensity_masked = np.where(mask_C, p_C_intensity, np.nan)
p_C_intensity_masked = p_C_intensity_masked[:, ~np.isnan(p_C_intensity_masked).any(axis=0)]
p_C_masked = p_C_intensity_masked[:2,:].astype(int)
intensity_masked = p_C_intensity_masked[2,:]
### compute hist
gray_masked_bin = self.images[i][p_C_masked[1,:], p_C_masked[0,:]] / self.bin_fraction
intensity_masked_bin = intensity_masked / self.bin_fraction
bins = self.num_bins
self.hist_handler.gray_hist += np.histogram(gray_masked_bin, bins=bins)[0]
self.hist_handler.intensity_hist += np.histogram(intensity_masked_bin, bins=bins)[0]
self.hist_handler.joint_hist += np.histogram2d(gray_masked_bin, intensity_masked_bin, bins=(bins, bins))[0]
self.hist_handler.gray_sum += gray_masked_bin.sum()
self.hist_handler.intensity_sum += intensity_masked_bin.sum()
self.hist_handler.total_points += len(gray_masked_bin)
Vectorizing step
1) projecting 3D point onto image: construct a matrix of 3D pointcloud coordinates, then do matrix operations with rotation matrix and translation vectorVectorizing step
2) validating projected point: concat projected pixels along with point intensities into one matrix, then use a mask to validateVectorizing step
3) computing histograms: update each histogram withnp.histogramthe whole vector of pixel intensity / lidar intensity
The complexity of this code is now only O(N)
To run this version, enter the following commands, either for I2I or D2D methods:
1
2
3
4
5
6
cd src/
# I2I
python script_I2I_vectorized.py
# or D2D
python script_D2D_vectorized.py
Note: You can plot mutual information scores over grids of extrinsic param pairs by uncommenting any of the following lines in the main script file
1
2
3
4
5
6
7
# calib.plot_MI(flag='010001') # y yaw
# calib.plot_MI(flag='100001') # x yaw
# calib.plot_MI(flag='110000') # x y
# calib.plot_MI(flag='010100') # y roll
# calib.plot_MI(flag='000101') # roll yaw
# calib.plot_MI(flag='000110') # roll pitch
# calib.plot_MI(flag='000011') # pitch yaw
Implementation Results
Mutual Information Scores
Indoor
Outdoor
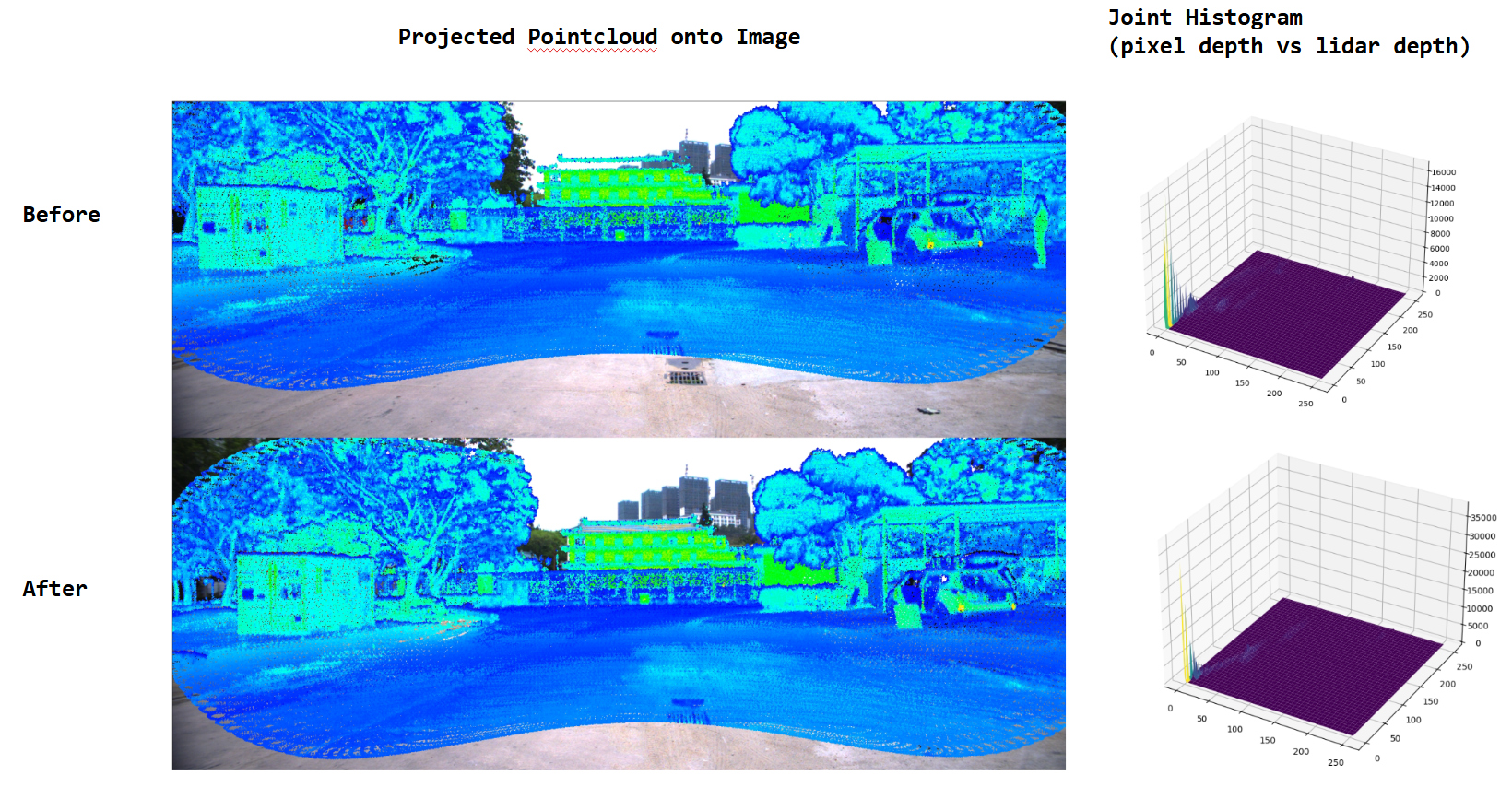
Before vs After calibration (D2D)
Indoor
Outdoor
Computation Time (per iteration)
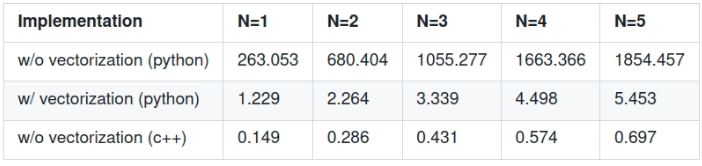Computation time for 1 iteration (seconds)
What’s next?
- C++ vectorized implementation
- Test on real Lidar, Camera
Thank you for reaching this point ^^